The Rabbit Riddle That Changed Math

How a medieval puzzle unlocked nature’s code…

In 1202, an Italian merchant’s son named Leonardo of Pisa published a book that would forever change the landscape of Western mathematics. Best known by his nickname Fibonacci, Leonardo is now remembered for something that seems deceptively simple — a sequence of numbers

This sequence emerged from a theoretical math problem and ended up revealing the golden thread of a pattern hidden in nature, art, architecture, and the very logic of growth itself, spanning disciplines, centuries and even civilizations.

This is the story of the Fibonacci Sequence, and it all starts with rabbits…

---

Reminder: To get our members-only content every week and support our mission, upgrade to a paid subscription for a few dollars per month. You’ll get:

• Two full-length, new articles every single week

• Access to the entire archive of useful knowledge that built the West

• Get actionable principles from history to help navigate modernity

• Support independent, educational content that reaches millions

---

The Problem in the Meadow

Fibonacci’s Liber Abaci (The Book of Calculation) was a groundbreaking text designed to introduce Hindu-Arabic numerals — 1 through 9, and the number 0 — to a Europe still using Roman numerals. The book was meant to help merchants and traders perform arithmetic faster, a task which proved difficult because of Roman numerals.

Tucked within its pages, however, is a now-famous problem:

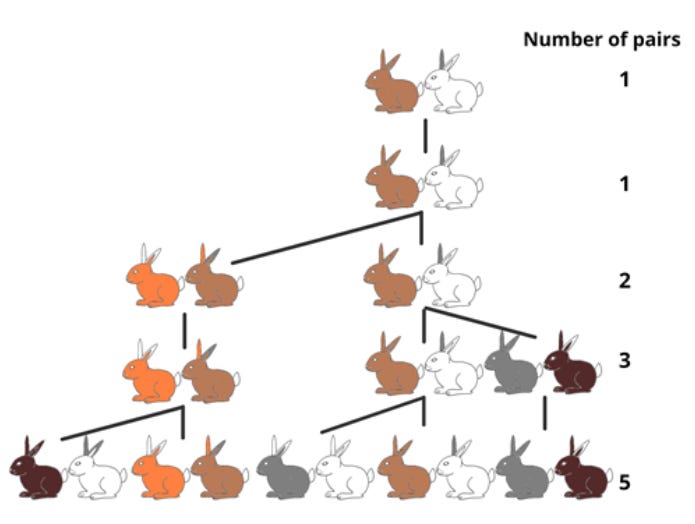
Suppose you place a pair of newborn rabbits into a field. Rabbits take one month to mature, and after that, each month, every mature pair produces one new pair of rabbits. How many rabbit pairs will there be after one year?

It’s just a thought experiment. No predators. No death. Only recursive reproduction. Let’s walk through the beginning:

• Month I: 1 pair (newborn)

• Month II: 1 pair (now mature)

• Month III: 2 pairs (the first produces another)

• Month IV: 3 pairs (the original pair produces again)

• Month V: 5 pairs

• Month VI: 8 pairs

• Month VII: 13 pairs

Each number in the sequence is the sum of the two before it.

A Sequence Is Born

The resulting series — 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... — is what we now call the Fibonacci Sequence. While Fibonacci popularized it in the West, the concept had already appeared around the world — including centuries earlier in India.

Ancient Indian mathematicians used the same recursive pattern while studying prosody (the rhythmic patterns in Sanskrit poetry.) Scholars like Virahanka (600 AD), Gopala (1135 AD), and Hemachandra (1150 AD) had discovered that the number of possible syllabic combinations in poetic meters followed the same logic.

So while Fibonacci didn’t invent the sequence, he helped spread its magic to Europe, where it was reborn — as a key to understanding patterns far beyond poetry or theoretical rabbits.

The Golden Ratio Emerges

Here the story gets even more fascinating. As the numbers grow, the ratio between each number and the one before it begins to reflect a very famous ratio.

Take a few examples:

• 3 / 2 = 1.5

• 5 / 3 ≈ 1.666

• 8 / 5 = 1.6

• 13 / 8 ≈ 1.625

• 21 / 13 ≈ 1.615

• 34 / 21 ≈ 1.619

The values approach 1.6180339887…, a ratio known as phi (φ) — the Golden Ratio. This ratio has a long history all of its own. It was studied by Euclid, admired by Renaissance artists, and embedded in the proportions of the natural world.

Mathematically, it’s defined by this elegant identity:

φ = (1 + √5) / 2

But the Fibonacci Sequence offers an intuitive way to approximate φ without any algebra — using simple addition.

Nature’s Hidden Geometry

The Golden Ratio and the Fibonacci Sequence often appear in nature.

Take a sunflower. If you count the spirals of seeds radiating out from the center, you'll often find Fibonacci numbers like 34, 55, or 89. The same is true in pinecones, pineapples, and the arrangement of leaves on a stem—a phenomenon known as phyllotaxis.

Why?

Because Fibonacci-based arrangements optimize space, exposure, and efficiency. In plants, it helps maximize sunlight absorption. In pineapples, it packs seeds tightly. Even hurricanes and galaxies often mimic the spiral structures of the Fibonacci Sequence and the Golden Ratio.

One could say that the Golden Ratio is one of God’s eternal perfect principles, which is imperfectly worked out by nature in the Fibonacci sequence — because no matter how far you take the Fibonacci sequence, it never arrives at the Golden Ratio.

Much like railroad tracks approaching the horizon — we know they don’t meet, but the further out they go, the more they seem to become one.

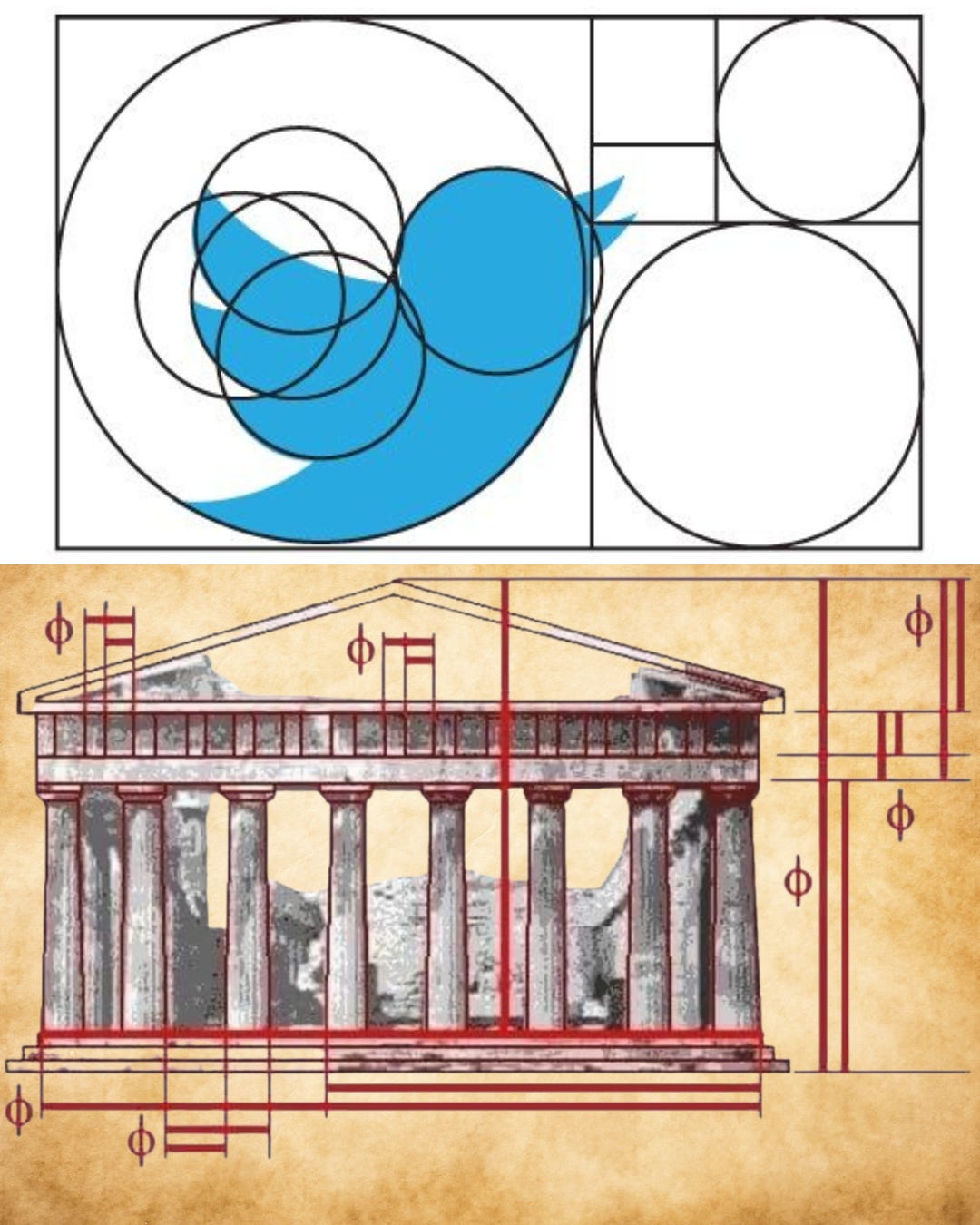
From Rabbits to Renaissance

Artists, too, have been drawn to these mathematical harmonies. The Golden Ratio has long been associated with aesthetic beauty. From the Parthenon to Leonardo da Vinci’s Vitruvian Man, and even modern logos — designers have turned to φ for visual balance.

Fibonacci’s work helped make these patterns visible and more easily understandable. What began as a simple math puzzle became a lens through which to interpret the structure of the universe—and our place within it.

The Sequence in Science and Tec

Beyond art and nature, the Fibonacci Sequence has found a home in computer science, financial modeling, and even music theory.

In programming, it teaches recursion — functions that call themselves — serving as a classic introductory problem in many coding courses, especially Python. In finance, Fibonacci retracement levels are used by traders to predict future market movements based on previous highs and lows. In music, composers have used Fibonacci numbers to structure phrasing and rhythm. Béla Bartók and the band Tool, though centuries apart, both referenced these patterns.

Even DNA molecules exhibit proportions close to the Golden Ratio in their helical structure. Whether you're looking at a pinecone or a double helix, the spiral form—closely linked to Fibonacci’s legacy—shows up again and again.

Why It Matters

So why should we care about a 13th-century rabbit riddle?

Because it reminds us that math is more than just equations on paper — it’s the grammar of God. A simple idea can unlock a world of structure, beauty, and interconnectedness. The Fibonacci Sequence symbolizes the power of pattern.

Fibonacci’s rabbits were theoretical, but their mathematical offspring are all around us: in the symmetry of sunflowers; in the rise and fall of financial markets; in the spirals of galaxies and seashells; in the compositions of artists and the calculations of engineers.

The Final Equation

At its heart, the Fibonacci Sequence is a lesson in growth, recursive logic, and natural design, but it's also something more poetic:

A reminder that within the simplest of stories — two rabbits in a field — we can discover the architecture and design of the cosmos, brought to us from one curious mind, and one enduring question: How fast do rabbits multiply?